(KDD 2020) Pro-GNN

Shuhan Song

2022-05-21

Paper Reading › Graph Neural Networks › Attacks and defends

paper:https://arxiv.org/abs/2005.10203

code:

GNN容易受到精心设计的干扰，称为对抗性攻击。对抗性攻击很容易欺骗GNN对下游任务进行预测。因此，开发鲁棒算法来防御对抗性攻击具有重要意义。防御对抗性攻击的一个自然想法是清除扰动图。很明显，真实世界的图具有一些固有的特性。例如，许多真实世界的图是低秩和稀疏的，并且两个相邻节点的特征往往相似。提出了一个通用框架Pro-GNN，它可以在这些属性的指导下，从扰动图中联合学习结构图和鲁棒图神经网络模型。

探索低秩和稀疏性属性

许多现实世界的图自然是低等级和稀疏的，因为实体通常倾向于形成社区，并且只与少数邻居相连，对GCN的对抗性攻击往往会增加连接不同社区节点的对抗性边缘，因为这样可以更有效地降低GCN的节点分类性能。因此，为了从有噪声和扰动的图中恢复干净的图结构，一种可能的方法是通过强制使用具有低秩和稀疏性的新邻接矩阵S来学习接近中毒图邻接矩阵的干净邻接矩阵。给定中毒图的邻接矩阵A，我们可以将上述过程表述为结构学习问题：

$\begin{equation} \mathop{\arg\min}_{S \in \mathcal S} \ \mathcal L_0 = \left\|A-S\right\|_F^2 + R(S) \quad s.t.,S=S^\mathsf{T} \end{equation}$

由于对抗性攻击的目标是对图形执行不可见的干扰，因此第一项$\left|A-S\right|_F^2$确保新邻接矩阵S应接近A，由于我们假设图是无向的，新邻接矩阵应是对称的，即$S=S^\mathsf{T}$, R(S)表示S上的约束，以增强低秩和稀疏性的性质，那R(S)该如何定义呢？根据一些研究，最小化矩阵的1范数和核范数可以分别强制矩阵稀疏和低秩。因此上式就可变为

$\begin{equation} \mathop{\arg\min}_{S \in \mathcal S} \ \mathcal L_0 = \left\|A-S\right\|_F^2 + \alpha \left\|S\right\|_1 +\beta \left\|S\right\|_* \quad s.t.,S=S^\mathsf{T} \end{equation}$

其中，$\alpha$和$\beta$是预定义的参数，分别控制稀疏性和低秩属性的贡献。最大限度地减少核范数$\left|S\right|_*$的一个重要好处是我们可以减少每一个奇异值，从而减轻对抗性攻击扩大奇异值的影响。

探索特征平滑度

很明显，图中的连接节点可能具有相似的特征。事实上，这种观察是在许多领域的图上进行的。例如，社交图中的两个连接用户可能共享相似的属性，网页图中的两个链接网页往往具有相似的内容，引文网络中的两篇连接论文通常具有相似的主题。同时，最近有证据表明，对图的对抗性攻击倾向于连接具有不同特征的节点。因此，我们的目标是确保所学习到的图中的特征平滑。特征平滑度可通过以下术语$\mathcal L_s$获得

$\begin{equation} \mathcal L_s = \frac{1}{2}\sum_{i,j=1}^{N}S_{ij}(x_i-x_j)^2 \end{equation}$

其中S是新的邻接矩阵，$S_{ij}$表示学习图中$v_i$和$v_j$的连接，以及$(x_i-x_j)^2$测量$v_i$和$v_j$之间的特性差异。$\mathcal L_s$可以重写为：

$\begin{equation} \mathcal L_s = tr(X^\mathsf{T}LX) \end{equation}$

其中$L=D− S$是$S$图的Laplacian矩阵，$D$是$S$的对角矩阵。在这项工作中，我们使用归一化Laplacian矩阵$\hat L=D^{-1/2}LD^{-1/2}$而不是L，以使特征平滑度独立于图形节点的度数，所以此时的$\mathcal L_s$就变成了如下的形式：

$\begin{equation} \mathcal L_s = tr(X^\mathsf{T}\hat LX) = \frac{1}{2}\sum_{i,j=1}^{N}S_{ij}(\frac{x_i}{\sqrt{d_i}} - \frac{x_j}{\sqrt{d_j}})^2 \end{equation}$

其中$d_i$表示学习图中$v_i$的阶数，在学习到的图中，如果$v_i$和$v_j$是连接的(即$S_{ij}\neq0$)，即特征差异$(x_i-x_j)^2$应较小。换言之，如果两个连接的节点之间的特征非常不同，$\mathcal L_s$非常大。因此，$\mathcal L_s$越小，图$\mathcal S$上的特征X越平滑。因此，为了实现所学习图中的特征平滑，我们应该最小化$\mathcal L_s$。因此，我们可以将特征平滑度项添加到的目标函数中，以惩罚相邻节点之间特征的快速变化，如下所示

$\begin{equation} \mathop{\arg\min}_{S \in \mathcal S} \ \mathcal L = \mathcal L_0 + \lambda\mathcal L_s =\mathcal L_0 + \lambda tr(X^\mathsf{T}LX) \quad s.t.,S=S^\mathsf{T} \end{equation}$

其中$\lambda$是一个预定义参数，用于控制特征平滑度的贡献。

Pro-GNN的目标函数

首先通过上面的式子从中毒图中学习一个图，然后用所学习的图训练GNN模型。然而，在这种两阶段策略下，对于给定任务的GNN模型，学习的图可能是次优的。因此，我们提出了一种更好的策略来联合学习特定下游任务的图结构和GNN模型。我们的经验表明，联合学习GNN模型和邻接矩阵优于两阶段。Pro-GNN的最终目标函数如下所示

1	简单说就是两阶段是先对图进行净化，再用这个图去训练GNN，而现在联合学习，一边训练一边优化

$\begin{equation} \mathop{\arg\min}_{S \in \mathcal S,\theta} \ \mathcal L = \mathcal L_0 + \lambda\mathcal L_s + \gamma\mathcal L_{GNN} = \left\|A-S\right\|_F^2 + \alpha \left\|S\right\|_1 +\beta \left\|S\right\|_* + \lambda tr(X^\mathsf{T}\hat LX) + \gamma\mathcal L_{GNN}(\theta,\mathcal S,X,\mathcal Y_L) \quad s.t.,S=S^\mathsf{T} \end{equation}$

该公式的另一个好处是，来自$\mathcal L_{GNN}$还可以指导图形学习过程，以抵御对抗性攻击，因为图形对抗性攻击的目标是最大化$\mathcal L_{GNN}$,所以我们在防御的时候要将这个值变小.

下面是Pro-GNN的整体框架图，非常的好理解

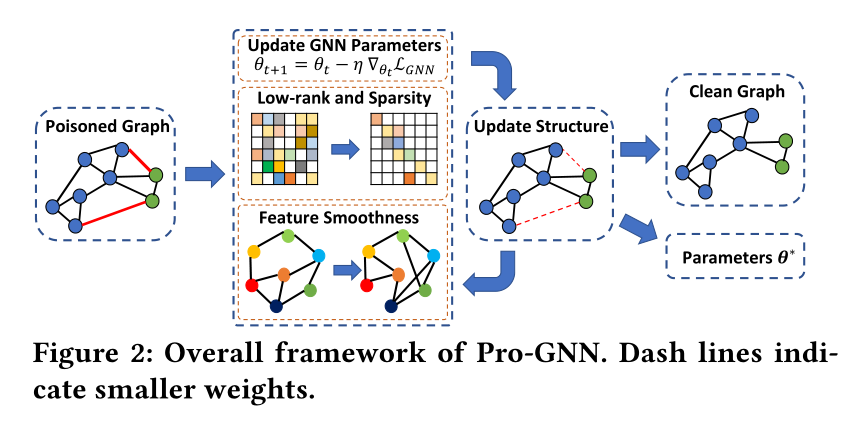
优化方法

联合优化等式上述等式中的$\theta$和$\mathcal S$是一项挑战。对$\mathcal S$的限制进一步加剧了这一困难。因此，在这项工作中，我们使用交替优化模式来迭代更新θ和S。

更新$\theta$

为了更新θ，固定S并删除与θ无关的项，然后目标函数减少为：

$\min_\theta \mathcal L_{GNN}(\theta,S,X,\mathcal Y_l) = \sum_{\mathcal u \in\mathcal V_L} \ell(f_\theta(X,S)_u,\mathcal y_u)$

这是一个典型的GNN优化问题，我们可以通过随机梯度下降来学习$\theta$。

更新$\mathcal S$

类似地，为了更新$\mathcal S$，我们固定$\theta$并得出

$\min_S \mathcal L(S,A) + \alpha \left\|S\right\|_1 +\beta \left\|S\right\|_* \quad s.t.,S=S^\mathsf{T}$

其中第一项为

$\mathcal L(S,A)= \left\|A-S\right\|_F^2 + \gamma\mathcal L_{GNN}(\theta,\mathcal S,X,\mathcal Y_L) + \lambda tr(X^\mathsf{T}\hat LX)$

请注意，ℓ1范数和核范数是不可微的。对于只有一个非微分正则化子R(S)的优化问题，我们可以使用前向-后向分裂方法（具体实现请看论文和代码）。想法是交替使用梯度下降步骤和近似步骤

总结：

本笔记重在理解两个部分

对中毒图的净化方法，包括控制低秩稀疏的$\ell_1$范数和核范数，还有特征平滑的方法
交替优化代替两阶段优化的优化方法